Scourges and Thorns and Nails -- Oh, my!

Remember, when we look at crucifixes, that it was our sins who put Him there.

The Way of the Cross - Station 3

Priest: The third station - Jesus falls the first time under His Cross

Genuflect

Priest: We adore Thee, O Christ, and we bless Thee.
People: Because by Thy Holy Cross Thou hast redeemed the world.

Stand

Priest: Consider this first fall of Jesus under His Cross, His flesh was torn by the scourges, His Head crowned with thorns, and He had lost a great quantity of Blood. He was so weakened He could scarcely walk; and yet He had to carry this great load upon his shoulders. The soldiers struck Him rudely, and thus He fell several times in His journey.

Kneel

People: My beloved Jesus, it is not the weight of the cross, but of my sins, which has made Thee suffer so much pain. Ah, by the merits of this first fall, deliver me from the misfortune of falling into mortal sin. I love Thee, O my Jesus, with my whole heart; I repent of having offended Thee. Never permit me to offend Thee again. Grant that I may love Thee always; and then do with me what Thou wilt.

Our Father . . . Hail Mary . . . Glory Be . . .

Priest: Lord, Jesus crucified!
People: Have mercy on us!

Stand

Christ above in torment hangs:
She beneath beholds the pangs
Of her dying glorious Son.

or

Quae moerebat, et dolebat,
Pia Mater dum videbat
Nati poenas incliti!

The cross bearer and acolytes proceed to the fourth station.

The Way of the Cross - Station 2

Priest: The second station - Jesus is made to bear His cross

Genuflect

Priest: We adore Thee, O Christ, and we bless Thee.
People: Because by Thy Holy Cross Thou hast redeemed the world.

Stand

Priest: Consider how Jesus, in making this journey with the Cross on His shoulders, thought of us, and offered for us to His Father the death He was about to undergo.

Kneel

People: My most beloved Jesus, I embrace all the tribulations Thou hast destined for me until death. I beseech Thee, by the merits of the pain Thou didst suffer in carrying Thy Cross, to give me the necessary help, to carry mine with perfect patience and resignation. I love Thee, Jesus, my Love; I repent of having offended Thee. Never permit me to separate myself from Thee again. Grant that I may love Thee always; and then do with me what Thou wilt.

Our Father . . . Hail Mary . . . Glory Be . . .

Priest: Lord, Jesus crucified!

People: Have mercy on us!

Stand

Oh, how sad and sore distressed

Was that Mother, highly blest,

Of the sole begotten One!

or

O quam tristis et afflicta

Fuit illa benedicta

Mater Unigeniti!

The cross bearer and acolytes proceed to the third station.

Suffragettes to Feminazis

1892:
Daisy, Daisy, give me your answer, do!
I'm half crazy all for the likes of you.
It won't be a stylish marriage,
I can't afford a carriage,
But you'd look sweet upon the seat
Of a bicycle built for two.

1992:
Davey, Davey, here is my answer true:
I'm not crazy all for the likes of you.
There won't be any marriage,
So don't go hire a carriage,
And I'll be damned if I'll be crammed
On a bicycle built for two!

Via Crucis - The Way of the Cross

According to St. Alphonsus Liguori

From a "Station Book" we used at St. Bridget's grade school in north Minneapolis when I was a kid in the 50's. We had Stations every Friday afternoon in Lent, right after school; attendance was not optional. The book was first published in 1936; mine is the 33rd edition, 1953, and the text and illustrations are taken from it.

To be said kneeling at the altar:

Priest and people:

My Lord Jesus Christ, Thou hast made this journey to die for me, with love unutterable, and I have so many times unworthily abandoned Thee; but now I love Thee with my whole heart, and because I love Thee, I repent sincerely for having offended Thee. Pardon me, my God, and permit me to accompany Thee on this journey. Thou goest to die for love of me; I wish also, my beloved Redeemer, to die for love of Thee. My Jesus, I will live and die always united to Thee.

Stand

At the cross her station keeping,

Stood the mournful Mother weeping,

Close to Jesus to the last.

or:

Stabat Mater dolorosa

Juxta Crucem lacrymosa

Dum pendebat Filius.

The cross bearer and acolytes with candles proceed to the first station.

Priest: The first station - Jesus is condemned to death

Genuflect

Priest: We adore Thee, O Christ, and we bless Thee.

People: Because by Thy Holy Cross Thou hast redeemed the world.

Stand

Priest: Consider how Jesus, after having been scourged and crowned with thorns, was unjustly condemned by Pilate to die on the Cross.

Kneel

People: My adorable Jesus, it was not Pilate, no, it was my sins that condemned Thee to die. I beseech Thee by the merits of this sorrowful journey, to assist my soul in its journey towards eternity. I love Thee, my beloved Jesus; I love Thee more than myself; I repent with my whole heart for having offended Thee. Never permit me to separate myself from Thee again. Grant that I may love Thee always; and then do with me what Thou wilt.

Our Father . . . Hail Mary . . . Glory be . . .

Priest: Lord, Jesus crucified!

People: Have mercy on us:

Stand

Through her heart, His sorrow sharing,

All His bitter anguish bearing,

Now at length the sword had passed.

or

Cujus animam gementem,

Contristatem et dolentem,

Pertransivit gladius.

The cross bearer and acolytes proceed to the second station.

The Cross is the Crux of the Matter

Prayer before a Crucifix

Behold, O kind and most sweet Jesus, I fall upon my knees before Thee, and with the most fervent desire of my soul I pray and beseech Thee that Thou wouldst impress upon my heart a lively sense of Faith, Hope, and Charity, with true contrition for my sins, and a firm purpose of amendment; whilst with deep affection and grief of soul, I ponder within myself and mentally contemplate Thy five most precious Wounds, having before my eyes that which David in prophecy spoke concerning Thyself, O good Jesus: "They have pierced my hands and feet, they have numbered all my bones."

Amen.

Isaiah 53

Who has believed what we have heard?

To whom has the arm of the Lord been revealed?

He grew up like a sapling before him, like a shoot from the parched earth;

there was in him no stately bearing to make us look at him,

nor appearance that would attract us to him.

He was spurned and avoided by men,

a man of suffering, accustomed to infirmity,

one of those from whom men hide their faces,

spurned, and we held him in no esteem.

Yet it was our infirmities that he bore,

our sufferings that he endured,

while we thought of him as stricken,

as one smitten by God and afflicted.

But he was pierced for our offenses,

crushed for our sins,

upon him was the chastisement that makes us whole,

by his stripes we were healed.

We had all gone astray like sheep, each following his own way,

but the Lord laid upon him the guilt of us all.

Though he was harshly treated,

he submitted and opened not his mouth;

like a lamb led to the slaughter or a sheep before the shearers,

he was silent and opened not his mouth.

Oppressed and condemned, he was taken away,

and who would have thought any more of his destiny?

When he was cut off from the land of the living,

and smitten for the sins of his people,

a grave was assigned him among the wicked,

and a burial place with evildoers,

though he had done no wrong nor spoken any falsehood.

But the Lord was pleased to crush him in infirmity.

If he gives his life as an offering for sin,

he shall see his descendants in a long life,

and the will of the Lord shall be accomplished through him.

Because of his affliction, he shall see the light in fullness of days;

through his suffering. my servant shall justify many,

and their guilt he shall bear.

Therefore I will give him his portion among the great,

and he shall divide the spoils with the mighty,

because he surrendered himself to death

and was counted among the wicked;

and he shall take away the sins of many,

and win pardon for their offenses.

The economic cost of abortion

Three years ago I did a study of lost wages that would have been paid to American workers (and the Social Security money collected on that, not to mention federal and state taxes) -- except that the workers were aborted between 1973 and 1990; and in 2007 the youngest of these lost workers would have been 17 and the oldest would have been 34.

This is wages only, mind you, not the school tuitions and fees paid, not the baby things bought (cradles, diapers, formula, baby food, baby clothes, car seats, etc.) , not the high school tuitions and activity fees, not the university tuitions, not the birthday cards and birthday cakes -- just wages only.

Between 1989 (when the 1973 babies turned 16) to 2003 (the last year for which I had good data) there were about $1.75 trillion dollars that were not paid out in wages, and about $59.4 billion dollars that the Soc. Sec. fund never saw.

And don't forget that it's almost certain that a good number of these lost babies would have grown up and had more babies, so the economic cost is actually worse than the above estimate.

And no one can tell me there's no connection between abortion, illegal immigration, and job outsourcing. Come on, folks, we're missing 52 million people! That's supposed to be without consequences?!

I'm sure that there are more complete data and better analyses out there. That said, I agree wholeheartedly with Alan Keyes when he says the number 1 economic problem in this country is not enough babies. See http://www.facebook.com/l.php?u=http%3A%2F%2Ftinyurl.com%2Fyg5o59d&h=269ae2e8fc4eec8da044958067e03cfd

This is money only.

Now I switch gears and say, "Money, shmoney! Babies are being killed and mothers are being almost-mortally wounded!" I know a few women who have had abortions, and they are deeply wounded and wish they hadn't. I know a couple of women who considered abortion, decided against it, and despite all the troubles (a Mom's middle name is "Worry") have never regretted choosing life.

The Bell Curve 4 - Correlation and Regression

These terms may look formidable, but they're actually simple: common sense set to mathematics, if you will. In the diagram in part 3, we see that high school seniors' heights are distributed in a pattern - not a perfect one, but a pattern all the same.

Now, says the book, have the guys line up on the gym floor in columns by height, and in rows by weight, and if you were up on the rafters, you would see a pattern like this one. You'll see at once that there's a relationship between height and weight: the shorter guys tend to be lighter than the taller guys. In statistics, this is called correlation; it's a very important concept, and highly important for the purposes of the book, because the authors do a great deal of correlating various data with general intelligence.

(We could add a third measurement -- waist size -- to the two we have, and have a three dimensional graph; where height is the first "input variable" x, weight is the second "input variable" y, and waist size is the "output variable" z. And, believe it or not, one can make a pretty good estimate of z, given x and y, IF one has a large enough sample. When doing things like this, the sample size is very very important.)

But to go back to this graph -- if one calculates the means and standard deviations of both height and weight, and redraws the graph in terms of means and standard deviations (rather than the raw data), one gets a new picture of the data, and one can then draw what's called the regression line or "best fit line," which is a picture of the mathematical relationship between height and weight -- both of which, be it noted, are expressed in their own terms (remember the elephants and cats).

This means that if you look at the distribution of the guys' weights for the mean height (again, assuming a large sample), you can make some solid statements about how likely it will be -- for instance -- that a guy of mean height will fall two standard deviations below the mean weight (for this sample, nobody).

From here I let the authors speak. This is from pp. 586-587 of the book, Appendix I, "Statistics for People Who Are Sure They Can't Learn Statistics." I'm quoting them because they say things better than I can.

"1. Notice the many exceptions. There is a statistically substantial relationship between height and weight, but, visually, the exceptions seem to dominate. So too with virtually all statistical relationships in the social sciences, most of which are much weaker than this one.

"2. Linear relationships don't always seem to fit very well. The best-fit line looks as though it is too shallow. [my note: a horizontal best fit line means, mathematically, no correlation between x and y.] Look at the tall boys, and see how consistently it [the line] underpredicts how much they weigh. Given the information in the diagram, this might be an optical illusion -- many of the dots in the dense part of the range are on top of each other, as it were, and thus it is impossible to grasp visually how the errors are adding up -- but it could also be that the relationship between height and weight is not linear.

"3. Small samples have individual anomalies. Before we jump to the conclusion that the straight line is not a good representation of the relationship, remember that this sample consists of only 250 boys. An anomaly of this particular small sample is that one of the boys in the sample of 250 weight 250 pounds. Eighteen-year-old boys are very rarely that heavy, judging from the entire NLSY [explained later] sample, fewer than one per 1,000. And yet one of those rarities happened to be picked up in a sample of 250. That's the way samples work.

[My note: and one of the reasons people go to garage and estate sales and show up on "Antiques Roadshow."]

"4. But small samples are also surprisingly accurate, despite their individual anomalies. The relationship between height and weight shown by the sample of 250 18-year-old males is identical to the third decimal place with the relationship among all 6,068 males in the NLSY sample. This is closer than we have any right to expect, but other random samples of only 250 generally produce correlations that are within a few hundredths of the one produced by the larger sample. (There are mathematics for figuring out what "generally" and "within a few hundredths" mean, but we needn't worry about them here.)"

So anyway -- what The Bell Curve is all about -- "Intelligence and Class Structure in American Life" -- is based on lots of mathematical analysis of quite a few numerically measurable factors about people. I hope I have shown how some of the analysis works. I think one can appreciate the book much better if one has an understanding of the tools Herrnstein and Murray used, to get the results and come to the conclusions they did.

All that said, I want to go on record that the numerically measurable factors about any human being are not, repeat not the most important things. Thinking they are, is the fallacy that agnostics and atheists fall into. We believers know better. Science is great in its place, but it can't explain everything.

New political party

There is a bold and daring new political party being formed in this country, which dares to declare its allegiance in its name. It is the Sacred Leader Obama Party.

If you really really love our president and what he's doing, get into the SLOP today!

"It Was a Very Good Year" -- so HE says

I had an untimely awakening this morning about 6:15, before first light, and while out on the porch with my after-breakfast see-gar (and bundled up against the +4F, -12C cold) a song that I heard maybe 44 years ago popped back into my head. The song was "It Was a Very Good Year" and the lyrics were:

When I was seventeen, it was a very good year,
It was a very good year for village girls and soft summer nights,
We'd hide from the lights on the village green,
When I was seventeen.

When I was twenty-one, it was a very good year,
It was a very good year for city girls who lived up the stair,
With perfumed hair that came undone,
When I was twenty-one.

When I was thirty-five, it was a very good year,
It was a very good year for blue-blooded girls of independent means,
We'd ride in limousines their chauffeurs would drive,
When I was thirty-five.

And now the days are short, I'm in the autumn of the year,
And I think of my life as vintage wine from fine old kegs,
From the brim to the dregs, it poured sweet and clear,
It was a very good year.

(The search engine says it was first recorded about 1965 and made a hit by Frank Sinatra. The search engine also turned up variations in the wording that are different from what I remember.)

The tune is romantic and haunting, and you see the rhyme scheme is a bit unusual. It has a pre-World-War-One air about it. It was a romantic song for a 21-year-old to listen to.

The 65-year-old thinking of the song says:

Hmm. How old is this guy? -- fifty? His "autumn" stops somewhere after thirty-five; he must have worn himself out seducing all those women. So okay, the song hints that maybe the "girls" didn't mind being seduced. All the same, I see precious little respect for the women. Admiration and fond memories, maybe; but really, the song's all about him and the fun he had. The guy is a hedonist, a rake, a roué, a Don Juan . . . in short a "bad hat" I wouldn't want any sister or daughter of mine being around.

I think it became a hit because of the temper of the times. It was 1965, and the antiwar and "flower power" movements were just getting going. And got stronger: the late sixties were a soap opera and a crazy quilt, and unbridled (I almost said un-bra-ed) hedonism was rampant: "If it feels good, do it."

And now a lot of the idiot kids who fell for all that crap are middle-aged hippie retreads, and a lot of them are in positions of power and influence. And that, friends, is one of the reasons this country is in such a mess today.

(Photo of protestors at the Democratic convention in Chicago, 1968)

The Bell Curve 3 - Centrality and variability

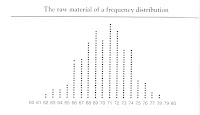We have seen from the last two posts that natural phenomena tend to cluster about some center, but with variation on how far the individual occurrences of the phenomenon fall from that center. This is called a frequency distribution. The concepts of frequency distribution, centrality and variability are of prime importance in statistics, so they're highly important to grasp, in order to understand how the authors of The Bell Curve reach the conclusions they get.

If you have a copy of the book, go to Appendix 1; Herrnstein and Murray say it better than I do. If not, above is an imagined overhead view of a high school senior class of guys (including girls would complicate matters in more ways than mathematically!) lined up in columns according to their height in inches:

We all have heard the word "average" many times: batting average, earned-run average, and so on. For everyday use the word is fine; for statistics it's not precise enough. The preferred term in statistics is "mean"; the mean is simply the sum of the occurrences of something divided by the number of occurrences. In the case of the high-school seniors, there are 250 guys, ranging in height from 5'2" to 6'6". The mean height (as a round number) is 70" or 5'10", calculated by multiplying each "x" (height) by its "y"+ (number of times x happens), and dividing that by the sum of the y's; that is, the sample size, n, 250. (to be precise, the mean height is about 70.26".)

This is a good example of how very many natural phenomena are distributed. There is a center, which can be calculated. There is distribution about the center, which is expressed in standard deviations. So what's a standard deviation? Basically, it's a measure of comparing apples to apples.

To quote the book: "When it comes to high school students, you have a good idea how big a six-inch difference is. But what does a six-inch difference mean when we are talking about the height of elephants? About the height of cats? It depends. And the things it depends on are the average height and how much height varies anong the things you are measuring. A standard deviation gives you a way of taking both that average and that variability into account, so that "6 inches" can be expressed in a way that means the same thing for high school students relative to other high school students, elephants relative to other elephants, and cats relative to other cats." (pp. 578-579; Emphasis theirs.)

Now a "true normal distribution," a perfect bell curve, is a mathematical abstraction, never observed exactly in nature. But if the sample of high school seniors were of 2500 boys, or 25,000 boys, or of 250,000 boys, the curve would tend to "smooth out" and approximate the ideal. In the mathematical ideal, the normal distribution extends to infinity in both directions, but for practical purposes, talking about populations of people, a normal distribution, or bell curve, is about six standard deviations (sd) wide, symmetrical, and centered on the mean.

The essential thing to remember is that in any normal distribution (or close approximation to it),
you will find that from the mean to +1sd or -1sd is 0.3413 or 34.13% of the population. Between 1sd and 2sd (either way) there will be 0.1359 or 13.59% of the population. Between 2sd and 3sd (again, either way) there will be 0.0213 or 2.13% of the population.

Add it all up -- 0.3413 + 0.3413 + 0.1359 + 0.1359 + 0.0213 + 0.0213 - and you get 0.997, which means that 99.7% of any distribution falls within the range -3sd to +3sd. The remaining three-tenths of one percent (three out of a thousand) fall outside this range. And as the authors explain, extremes tend to be rarer than the average. "It is worth pausing a moment over this link between a relatively simple measure of spread in a distribution and the way things in everyday life vary, for it is one of nature's more remarkable uniformities." (p.581)

Or as I like to say, as the understatement of the cosmos, "God is pretty smart."

In case this is discouraging anyone, it has taken me about four hours to write this; and it also happens that I started reading Peter Kreeft's A Shorter Summa last week, so I have to learn a whole new vocabulary too.

But we're getting close to the book. The only thing I see a need to talk about first are the concepts of regression and correlation. I bet you just can't wait!

Thoughts while watching it snow

I went outside with my breakfast coffee to have my filthy evil see-gar, and while watching it snow (it's +12F, -10C), it occurred to me . . .

"Now at this time Caesar Augustus issued a decree for a census of the whole world to be taken. This census -- the first -- took place while Quirinus was governor of Syria, and everyone went to his own town to be registered. So Joseph set out from the town of Nazareth in Galilee and traveled up to Judaea, to the town of David called Bethlehem, since he was of David's house and line, in order to be registered together with Mary, his betrothed, who was with child."

According to Jim Bishop (The Day Christ Died and The Day Christ was Born) it is about ninety miles from Nazareth to Bethlehem, and the Holy Family traveled this on foot (well, Jesus didn't, but you know what I mean).

And for what?

The spiritual reason they went to Bethlehem was so Jesus would be born there, to fulfill the prophecy, of course. (That should go without saying.)

The worldly reason they went there, was so Caesar Augustus would know how many subjects he had, so he could tax them.

Even had he known about this young carpenter and his very pregnant wife traveling ninety miles on foot, would he have cared? Somehow I doubt it. Caesar didn't give orders for his subjects' convenience.

And that, folks, is what imperial government is like. It sure isn't "of the people, by the people, and for the people."

The Bell Curve 2 - what looks random maybe isn't

Here is a picture of my hand holding my little basket-like bathroom sink drain filter. I got curious a few years ago, and wondered if I held it like that, gave it a flip like a coin and let it bounce around inside the sink, whether it would seat itself perfectly in the drain hole. I knew it would get close to the drain, because of the shape of the sink -- but would it seat itself perfectly? I thought not: there were too many other ways it could end up.

So I started an experiment. I would flip the thing ten times, and see how many times out of ten flips it would seat itself perfectly. The results surprised me. In 187 trials of ten flips each, the numbers came out to be:

0 "perfect seatings" - 0 occurrences
1 ps - 2 occurrences
2 ps - 6
3 ps - 15
4 ps - 35
5 ps - 51
6 ps - 43
7 ps - 24
8 ps - 11
9 ps - 0
10 ps - 0

Note especially here that the data form a bell-shaped curve which is almost symmetrical. There is a pattern in what looks like randomness or chaos. I won't bore you with the math used to compute the "expected value" of X, the number of perfect seatings out of ten flips, but the answer, given the data, is about 5.18, which means that on average, in general, there is a slightly better than even chance that on any given flip, the strainer will seat itself perfectly.

Here's another example, a game called "coincidences." You shuffle a deck of cards, cut it, and deal thirteen cards off the top; as you lay down the first card, you say "ace"; as you lay down the second card, you say "deuce," as you lay down the third, you say "trey," and so on up to jack, queen, and king. The question is: what is the chance that you'll get at least one "coincidence" as you lay out the cards -- that, for example, as you say "six" you turn up a six? It would seem far-fetched -- until you do it. I played the game 150 times and got:

zero coincidences 54 times
one coincidence 56 times
two coincidences 29 times
three coincidences 9 times
four coincidences 2 times

which means the odds (chance, probability) of getting at least one coincidence are slightly under 2/3; for this group of trials, p(x) = 0.6204. Note "p(x)" means "probability of x happening," where p by definition is a decimal between 0 and 1, where 0 means impossibility and 1 means certainty.

(I mention in passing that this game can be used to win beers at your local watering hole, because the results are counter-intuitive. You never heard me say this.)

And of course a pattern strongly implies a pattern-Maker.